Students can Download Basic Maths Exercise 1.6 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 1 Matrices and Determinants Ex 1.6
Part – A
2nd PUC Basic Maths Matrices and Determinants Ex 1.6 Two or Three Marks Questions and Answers
Note:
Adjoint of a second order square matrix is obtained by interchanging principal diagonal elements & changing the signs of the secondary diagonal elements.
Question 1.
Find the adjoint of the following Matrices
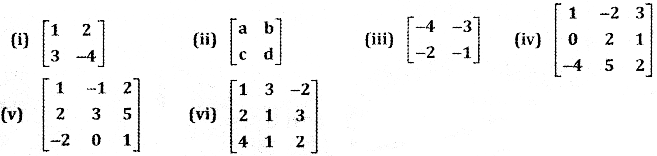
Answer:

![]()


![]()
Question 2.
Verify A. adjA = adjA. A = | A| . I for the following Matrices.

Answer:


![]()



![]()



![]()
Question 3.
Verify adj (A,B) = adjB . adjA for the following matrices.
Answer:


![]()


![]()
Question 4.
If A = \(\left[ \begin{matrix} 1 & -1 & 3 \\ -2 & 4 & 1 \\ 5 & -4 & 0 \end{matrix} \right]\) and B = \(\left[ \begin{matrix} 2 \\ -1 \\ 4 \end{matrix} \right]\) then find (adj A).B
Answer:

Question 5.
If A = \(\left[ \begin{matrix} 1 & -1 & 1 \\ 2 & 3 & 0 \\ 18 & 2 & 10 \end{matrix} \right]\) . show that A. adjA = 0
Answer:

![]()
Question 6.
Find the inverse of the following matrices.

Answer:


![]()



![]()
Question 7.
If A = \(\left[ \begin{matrix} 2 & 3 \\ 1 & -4 \end{matrix} \right]\) B = \(\left[ \begin{matrix} 1 & -2 \\ -1 & 3 \end{matrix} \right]\). Verify that (AB)-1 = B-1A-1
Answer:

From (1) & (2) we have (AB)-1 = B-1 . A-1.
Question 8.
If A = \(\left[ \begin{matrix} 3 & -5 \\ -4 & 2 \end{matrix} \right]\) . verify that A2 – 5A – 14I = 0 and hence find A-1.
Answer:

A2 – 5A – 14I = 0 Premuliply by A-1
A-1A A – 5A-1A – 14A-1 I= 0
IA – 5I – 14A-1 = 0
A – 5I – 14A-1 = 0
A – 5I – 14A-1
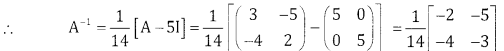
![]()
Question 9.
If A = \(\left[ \begin{matrix} 1 & 1 \\ 2 & 3 \end{matrix} \right]\) . Show that A2 – 4A + 51 = 0. Hence obtain A-1.
Answer:

![]()
Question 10.
If \(\left[ \begin{matrix} 5x & 2 \\ -10 & 1 \end{matrix} \right]\) is a singular matrix. Find x.
Answer:
