2nd PUC Maths Model Question Paper 4 with Answers

Students can Download 2nd PUC Maths Model Question Paper 4 with Answers, Karnataka 2nd PUC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Maths Model Question Paper 4 with Answers

Time: 3 Hrs 15 Min
Max. Marks: 100

Part-A

Answer all the questions: (10 × 1 = 10)

Question 1.
Let * be a operation defined on the set of rational numbers by a* b = \(\frac{\mathrm{ab}}{4}\) find the identify element.
Answer:
a*e = e*a=a

e = 4

Question 2.
Write the values of x for which 2 tan^-1 x = cos^-1\(\frac{1-x^{2}}{1+x^{2}}\) holds
Answer:
x ≥ 1

Question 3.
Construct a 2 × 2 matrix A = [a_ij] whose elements are given by \(\frac{1}{2}|-3 i+j|\)
Answer:
A = \(\left[ \begin{matrix} 1 & 1/2 \\ 5/2 & 2 \end{matrix} \right] \)

Question 4.
Find the values of x for which \(\left| \begin{matrix} 3 & x \\ x & 1 \end{matrix} \right| \) = \(\left| \begin{matrix} 3 & 2 \\ 4 & 1 \end{matrix} \right|\)
Answer:

x² = 8
x = ± \(\sqrt{8}\) = ± 2\(\sqrt{2}\)

Question 5.
Find \(\frac{d y}{d x}\), if y = sin (x² + 5)
Answer:
\(\frac{d y}{d x}\) = cos(x² + 5).2x

Question 6.
Evaluate : \(\int e^{x}\left(\frac{x-1}{x^{2}}\right) d x\)
Answer:
\(=\int e^{x}\left(\frac{1}{x}-\frac{1}{x^{2}}\right) \cdot d x=e^{x}\left(\frac{1}{x}\right)+c\)

Question 7.
Define negative of a vector.
Answer:
Negative vector is a vector whose magnitude is same with opposite direction

Question 8.
Write the direction cosines of x – axis.
Answer:
1, 0, 0

Question 9.
Define feasible region in LPP.
Answer:
The common region determined by all the constraints including non-negative constraints.

Question 10.
If P(A) = \(\frac { 3 }{ 5 }\), P(B) = \(\frac { 1 }{ 5 }\)
find p(A ∩ B) if A and B are independent events
Answer:
p(A ∩ B) = p(A), p(B)
p(A ∩ B) = \(3 / 5 \cdot 1 / 5\) = \(\frac { 3 }{ 25 }\)

Part-B

Answer any ten questions: (10 × 2 = 20)

Question 11.
Show that if f: A → B and g: B → C are one – one, then gof : A → C is also one – one
Answer:
gof (x₁) = gof(x₂)
g[f(x₁)]=g[(x₂)]
f(x₁) = f(x₂)
x₁ = x₂
since g and f is one – one, gof is one – one

Question 12.
Show that
sin^-1 \((2 x \sqrt{1-x^{2}})\) = 2sin^-1 x for \(\frac{-1}{\sqrt{2}} \leq x \leq \frac{1}{\sqrt{2}}\)
Answer:
Let x = sin θ ⇒ θ = sin^-1 x
2x \(\sqrt{1-x^{2}}\) = 2 sin θ \(\sqrt{1-\sin ^{2}} \theta\)
2 sin θ. cos θ = sin 2θ
⇒ sin^-1 (2x\(\sqrt{1-x^{2}}\))
= sin^-1(sin 2θ) = 2 sin^-1 x

Question 13.
Show that
2 tan^-1 \(\frac { 1 }{ 2 }\) + tan^-1 \(\frac { 1 }{ 7 }\) = tan^-1 \(\frac { 31 }{ 17 }\)
Answer:

Question 14.
If the area of the triangle with vertices (-2,0),(0,4) and (0,k) is 4 square units, find the values of k using determinants.
Answer:

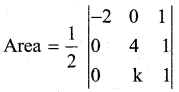
±4 = \(\frac { 1 }{ 2 }\) {-2 (4 – k) + (0) }
±4 = K – 4
+4 = k – 4 -4 = k – 4
k = 4 + 4 k = 0
k = 8

Question 15.
Differentiate \(\left(x+\frac{1}{x}\right)^{x}\) with respect to x,
Answer:

Question 16.
Find the slope of the tangent to the curve y = \(\frac{\mathbf{x}-1}{\mathbf{x}-2}\) x ≠ 2 at x = 0
Answer:

Question 17.
Find \(\frac{d y}{d x}\), if x² + xy + y² = 100
Answer:
2x + x\(\frac{d y}{d x}\) + y + 2y \(\frac{d y}{d x}\) = 0
(x + 2y)\(\frac{d y}{d x}\) = -(2x + y)
\(\frac{d y}{d x}=\frac{-(2 x+y)}{x+2 y}\)

Question 18.
Evaluate :\(\int \frac{\cos 2 x-\cos 2 \alpha}{\cos x-\cos \alpha} d x\)
Answer:
\(=\int \frac{\left(2 \cos ^{2} x-1\right)-\left(2 \cos ^{2} \alpha-1\right)}{\cos x-\cos \alpha}, d x\)
\(=\int 2 \frac{(\cos x-\cos \alpha)(\cos x+\cos \alpha)}{\cos x-\cos \alpha}, d x\)
\(=2 \int \cos x+\cos \alpha, d x\)
= 2 sin x + 2x cos α + c

Question 19.
Evaluate \(\int \frac{d x}{x-\sqrt{x}}\)
Answer:

Question 20.
Find the order and degree, if defined of the differential equation
\(\left(\frac{\mathbf{d}^{2} \mathbf{y}}{\mathbf{d x}^{2}}\right)^{3}+\left(\frac{\mathbf{d y}}{\mathbf{d x}}\right)^{2}+\sin \frac{\mathbf{d y}}{\mathrm{dx}}+1=\mathbf{0}\)
Answer:
order is 2
degree is not defined

Question 21.
Find \(|\overrightarrow{\mathrm{b}}|\), if \((\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=8\) and \(|\overrightarrow{\mathrm{a}}|\) = 8\(|\overrightarrow{\mathrm{b}}|\)
Answer:

Question 22.
Find the area of the parallelogram whose adjacent sides are determined by the vectors \(|\overrightarrow{\mathrm{a}}|\) = î – ĵ + 3k̂ and \(|\overrightarrow{\mathrm{b}}|\) = 2î – 7ĵ + k̂
Answer:

Question 23.
Find the angle between the pair of lines given by
\(|\overrightarrow{\mathrm{r}}|\) = 3î + 2ĵ – 4k̂ + λ(î + 2ĵ + 2k̂) and \(|\overrightarrow{\mathrm{r}}|\) = 5î – 2ĵ + µ(3î + 2ĵ + 6k̂)
Answer:

Question 24.
Let X denote the number of hours you study during a randomly selected school day. The probability that X can take the values of x, has the following form, where k is some constant

find the value of k.
Answer:
ΣP(x) = 1

k = \(\frac { 1 }{ 5 }\)

Part-C

Answer any ten questions: (10 × 3 = 30)

Question 25.
Determine whether the relation R in the set A = {l,2,3, ……… 13,14} defined as R = {(x,y) : 3x = y = o}, is reflexive, symmetric arid transitive.
Answer:
y = 3x
R – {(1,3) (2,6) (3, 9) (4,12)}
R is not reflexive as (l,l) ∉ R
R is not symmetric as
(1,3) ∈ R but (3,1) ∉ R
R is not transitive as
(1,3) ∈ R, (3,9) ∈R but (l,9)∉ R

Question 26.
If tan^-1 \(\frac{x-1}{x-2}\) + tan^-1 \(\frac{x+1}{x+2}\) = \(\frac{\pi}{4}\) , then find the values of x.
Answer:

Question 27.
If A and B are invertible matrices of the same order, then prove that (AB)^-1 = B^-1 A^-1.
Answer:
From definition of inverse of matrix
(AB) (AB)^-1 =1
A^-1 (AB)(AB)^-1 = A^-1l
(A^-1A) B(AB)^-1=A^-1.
IB (AB)^-1 = A^-1
B(AB)^-1 = A^-1
B^-1B(AB)^-1 = B^-1 A^-1
l(AB)^-1 = B^-1 A^-1
(AB)^-1 = B^-1A^-1

Question 28.
verify Rolles theorem for the funciton f(x)= x² + 2X – 8, x ∈[-4,2]
Answer:
f (x) =x² +2x – 8
1. f (x) being a polynominal function it is continuous on (-4,2)
2. Also f¹ (x) = 2x + 2 hence derivable on (-4,2)
3. f(-4) = (-4)² + 2(-4) -8 = 0
f(2) = 2² + 2(2) – 8 =0
∴ f(-4) = f(2)
∴ All three conditions of Rolle’s theorem are verified.
f¹ (c) = 0
f¹ (c) = 2c + 2 ⇒ 0 = 2c + 2
⇒ c = -1 ∈(-4,2)

Question 29.
If x = \(\sqrt{\mathbf{a}^{\sin ^{-1} \mathbf{t}}}\) and \(\sqrt{\mathbf{a}^{\cos ^{-1} \mathbf{t}}}\) then prove that \(\frac{d y}{d x}=\frac{-y}{x}\)
Answer:

Question 30.
Find the two positive numbers whose sum is 15 and sum of whose squares is minimum.
Answer:
x + y = 15 ⇒ y = 15 – x
s = x² + y² ⇒ s = x² + (15 – x)²
\(\frac{d s}{d x}\) = 2x + 2(15 – x) (-1)
\(\frac{d s}{d x}\) = 0 2x – 30 + 2x
0 = 4x – 30
x = \(\frac { 30 }{ 4 }\) = 7.5
\(\frac{d^{2} s}{d x^{2}}=2+2=4>0\)
∴ x = 7.5 require no is y = 7.5 & x = 7.5

Question 31.
Evaluate : \(\int x \tan ^{-1} x d x\)
Answer:

Question 32.
Evaluate \(\int_{0}^{2} e^{x}\) dx as a limit of a sum
Answer:
\(\int_{0}^{2} e^{x}\) .dx
= \(\left.e^{x}\right]_{0}^{2}\) = e² – e⁰ = e² – 1

Question 33.
Find the area of the region bounded by the curve y² = 4x and the line x = 3
Answer:

Question 34.
Show that the position vector of the point P, which divides the line joining the points A and B having position vectors \(\overrightarrow{\mathrm{a}}\) and \(\overrightarrow{\mathrm{b}}\) internally in the ratio m : n is \(\frac{m \vec{b}+n \vec{a}}{m+n}\)

Answer:
‘O’ is the fixed point, \(\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}}\)
\(\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{b}}\) P divides the line AB internally in the ratio m : n

Question 35.
Show that the four points with position vectors 4î + 8ĵ + 12k̂, 2î + 4ĵ + 6k̂, 3î + 5ĵ + 4k̂ and 5î + 8ĵ + 5k̂ are coplanar.
Answer:

Question 36.
Find the equation of the plane passing through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z + 2=0 and the point (2,2,1)
Answer:
Equation of plane passing through intersection of the plane is
(3x – y + 2z – 4) + λ (x + y + z + 2) = 0 This plane pass through (2,2,1)
3(2) – 2 + 2(1) -4 + λ(2 + 2 + 1 + 2)=0
2 + 7λ = 0
λ = \(\frac { -2 }{ 7 }\)
Required equqtion of plane is
(3x – y + 2z – 4) + \(\left(\frac{-2}{7}\right)\) (x + yz + 2) + 0 [x^ly by 7]
21x – 7y + 14z – 28 – 2x – 2y – 2z – 4 = 0
19x – 9y + 12z = 32

Question 37.
Form the differential equation of the circles touching the x – axis at origin.
Answer:
(x – h)² +(y – k)² = r²
(x – 0)² +(y – k)² =a²
x² + y² = 2ay ⇒ 2a = \(\frac{x^{2}+y^{2}}{y}\)
diff Equ w.r. to x

Question 38.
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01,0.03 and 0.15 respectively. One of the insured person meets with an accidents. What is the probability that he is a scooter driver?
Answer:

Part-D

Answer any six questions: (6 × 5 = 30)

Question 39.
Let R₊ be the set of all non- negative real numbers. Show that the function f: R₊ → [4,∞)given by f(x) = x² +4 is invertible and write the inverse of f.
Answer:
f(x₁) = f(x₂)
X₁² + 4 = X₂² + 4
x₁ = x₂ ∴ f (x) is one-one
Let y = f(x)
y = 4x +3
x = \(\frac{y-3}{4}\) ∈R₊ ∴ f (x) is onto
Let
f^-1 (x) = y
f(y) = x
4y +3 =x
\(y=\frac{x-3}{4}\)
∴ f^-1 : [4,8) → R₊ is defined by
f^-1 (x) = \(\frac{x-3}{4}\)

Question 40.
If A = \(\left[ \begin{matrix} 1 & 2 & 3 \\ 3 & -2 & 1 \\ 4 & 2 & 1 \end{matrix} \right]\) , then show that A³ -23A -40I = 0
Answer:

Question 41.
Solve by Matrix method :
2x + 3y + 3z = 5
x – 2y + z = 5
3x – y – 2z = 3
Answer:

Question 42.
If y = Ae^mx + Be^nx show that \(\frac{d^{2} y}{d x^{2}}\) -(m + n) \(\frac{d y}{d x}\) + mny = 0
Answer:
\(\frac{d y}{d x}\) = Ame^ex + Bne^xn
\(\frac{d^{2} y}{d x^{2}}\) = Am²e^mx + Bn²e^nx
\(\frac{d^{2} y}{d x^{2}}\) – (m + n) \(\frac{d y}{d x}\) + my
= Am²e^mx+ Bn²e^nx – m²Ae^mx – Amne^mx – Bn²e^nx – mnBeⁿⁿ + Amne^mx + mnBe^nx = 0

Question 43.
A particle moves along the curve 6y = x³ + 2. Find the points on the curve at which the y – coordinate is changing 8 times as fast as the x – coordinate.
Answer:
6y = x³ + 2 → (l)
\(\frac{d y}{d x}=\frac{x^{2}}{2}\)
Given that \(\frac{d y}{d t}\) = 8 \(\frac{d x}{d t}\) ⇒ \(\frac{d x}{d t}\) = 8
∴ 8 = \(\frac { 1 }{ 2 }\) x²
x = ±4
put x in Equation (01) 6y = 4³ + 2
∴ x = 4 y = 11
∴ x = -4 , 6y = (-4)³ + 2 ⇒ y = -10,3 points are (4,11) (-4, -10,3)

Question 44.
Find the integral of \(\frac{1}{\sqrt{x^{2}-a^{2}}}\) with respect to x and hence evaluate \(\frac{d x}{\sqrt{x^{2}+6 x-7}}\)
Answer:

Question 45.
Using integration find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4

Answer:
y = 2x – 1
points are (0,1) (1,3) (4,9) etc
x = 4, (4,0) (4,1) (4,2) etc
Area = \(\int_{0}^{4}(3 x+1), d x-\int_{0}^{4}(2 x+1), d x\)
\(A=\left(\frac{3 x^{2}}{2}+x\right)^{4}-\left(\frac{2 x^{2}}{2}+x\right)^{4}\)
A = 24 + 4 – 16 – 4 = 8 sq units

Question 46.
Solve the differential equation \(\frac{d y}{d x}+y\) sec x = tan x,0 ≤ x < \(\frac{\pi}{2}\)
Answer:
P = secx Q = tan x
IF = \(e^{\int \sec x d x}=e^{\log (\sec x+\tan x)}\) = secx + tanx
y x IF = ∫ Q x IF
y (sec + tan x) = ∫(sec x + tan x) tan x.dx = ∫sec x.tan x + ∫ tan² x.dx
=secx + ∫(sec² x – 1) dx
y(sec x+tan x) = sec x + tan x – x + c

Question 47.
Derive the equation of the line in space passing through a point and parallel to a vecor both in vector and Cartesian form.
Answer:

Let ‘A’ be the point, \(\overrightarrow{\mathrm{a}}\) is P V of \(\overrightarrow{\mathrm{A}}\)
\(\overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{r}}-\overrightarrow{\mathrm{a}}\)
AP is parallel to vector \(\overrightarrow{\mathrm{b}}\)
\(\overrightarrow{\mathrm{AP}}=\lambda \overrightarrow{\mathrm{b}}\)
\(\overrightarrow{\mathrm{r}}-\overrightarrow{\mathrm{a}}=\lambda \overrightarrow{\mathrm{b}}\)
\(\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}+\lambda \overrightarrow{\mathrm{b}}\) is vector form
A=(x₁ y₁, z₁) p (x,y,z) \(\overrightarrow{\mathrm{b}}\) =b₁i+b₂j+b₃k
Now \(\overrightarrow{\mathrm{r}}\) = xi + yj + zk, \(\overrightarrow{\mathrm{a}}\) =x₁i + y₁j + z₁k
\(\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}+\lambda \overrightarrow{\mathrm{b}}\) takes the form
xi + yj + zk=(x₁i + y₁j + z₁k) + λ(b₁i + b₂j + b₃k)
xi + yj + zk=(x₁ +λb₁)i+(y₁ +λb₂) j + (z₁+ λb₃)k
x =X₁ +λb₁ y= y₁ + λb₂ z = z₁ + λb₃

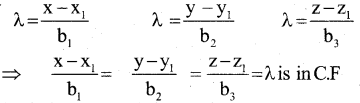
Question 48.
A die is thrown 6 times. If ‘getting an odd number’is a success, what is probability of:
a) 5 successes?
Answer:
\(P(5)=6_{c_{3}}\left(\frac{1}{2}\right)^{6-5}\left(\frac{1}{2}\right)^{5}=6\left(\frac{1}{2}\right)\left(\frac{1}{32}\right)=\frac{3}{32}\)

b) at least 5 successes?
Answer:
\(P(x \geq 5)=P(5)+P(6)=\left(\frac{1}{2}\right)^{6}\left[6_{C_{5}}+6_{C_{6}}\right]=\frac{6}{64}+\frac{1}{64}=\frac{7}{64}\)

c) at most successes?
Answer:
P(X≤ 5) = P(0) + P(1) + P(2) + P(3) + P(4) + P(5) = \(\left(\frac{1}{2}\right)^{6}\) [1 + 6 + 15 + 20 + 15 + 6] = \(\frac { 63 }{ 64 }\)

Part-E

Answer any one question : (1 × 10 = 10)

Question 49.
a) Prove that

and hence evaluate \(\int_{-1}^{1} \sin ^{5} x \cos ^{4} x d x\)
Answer:

f(x) = sin⁵x.cos⁴x
f(-x) = sin⁵(-x) cos⁴(-x) = -sin⁵x.cos⁴x = -f(x)
∴ f is odd function, I = 0

b) prove that \(\left| \begin{matrix} { a }^{ 2 }+1 & ab & ac \\ ab & { b }^{ 2 }+1 & bc \\ ca & cb & { c }^{ 2 }+1 \end{matrix} \right| \) = 1 + a² + b² + c²
Answer:

Question 50.
a) A manufacturing company makes two models A and B of a product. Each piece Of model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of model B requires 12 labour hours for finishing and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of Rs. 8,000 on each piece of model A and Rs. 12,000 on each piece of model B. How many pieces of model A and model B should be manufactured per week to realize a maximum profit? What is the maximum profit per week?
Answer:

Z = 8000x + 12000y
ax + 12y ≤ 180 ⇒ 180 ⇒ 3x + 4y ≤ 160
x + 3y ≤ 30

b)
Find the value of K so that the function

continuous function.
Answer: