Students can Download Maths Chapter 5 Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 5 Continuity and Differentiability Miscellaneous Exercise
2nd PUC Maths Chapter 5 Continuity and Differentiability NCERT Text Book Questions and Answers Miscellaneous Exercise
Differentiate w.r.t. x the function in Exercise 1 to 11.
Question 1.
(3x2 – 9x + 5)9
Answer:

Question 2.
sin3 x + cos6 x
Answer:

![]()
Question 3.
(5x)3cos2x
Answer:


Question 4.
\(\sin ^{-1}(x \sqrt{x}), 0 \leq x \leq 1\)
Answer:

Question 5.
\(\frac{\cos ^{-1}\left(\frac{x}{2}\right)}{\sqrt{2 x+7}},-2<x<2\)
Answer:


![]()
Question 6.
\(\cot ^{-1}\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right], 0<x<\frac{\pi}{2}\)
Answer:

Question 7.
(log x)log x ,x > 1
Answer:

Question 8.
cos (a cos x + b sin x), for some constant a and b.
Answer:

Question 9.
\((\sin x-\cos x)^{(\sin x \cdot \cos x)}, \frac{\pi}{4}<x<\frac{3 \pi}{4}\)
Answer:

![]()
Question 10.
xx + xn + ax + an, for some fixed a > x and x > 0
Answer:

Question 11.
\(x^{x^{2}-3}+(x-3)^{x^{2}}, \text { for } x>3\)
Answer:


Question 12.
Find
\(\frac{d y}{d x}, \text { if } y=12(1-\cos t), x=10(t-\sin t),-\frac{\pi}{2}<t<\frac{\pi}{2}\)
Answer:

![]()
Question 13.
Find
\(\frac{d y}{d x}, \text { if } y=\sin ^{-1} x+\sin ^{-1} \sqrt{1-x^{2}},-1 \leq x \leq 1\)
Answer:

Question 14.
If \(x \sqrt{1+y}+y \sqrt{1+x}=0 \text { for },-1<x<1, \text { prove that } \frac{d y}{d x}=-\frac{1}{(1+x)^{2}}\)
Answer:


Question 15.
If (x – a)2 + (y – b)2 = c2, for some c > 0, prove that
\(\frac{\left[1+\left(\frac{\mathrm{dy}}{\mathrm{d} \mathbf{x}}\right)^{2}\right]^{\frac{3}{2}}}{\frac{\mathbf{d}^{2} \mathbf{y}}{\mathbf{d x}^{2}}}\)
Answer:

![]()
Question 16.
If cos y = x cos (a + y), with cos a ≠ ± 1, prove that
\(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}\)
Answer:


Question 17.
If x = a (cos t + t sin t) and y = a (sin t -1 cos t), find \(\frac{d^{2} y}{d x^{2}}\)
Answer:
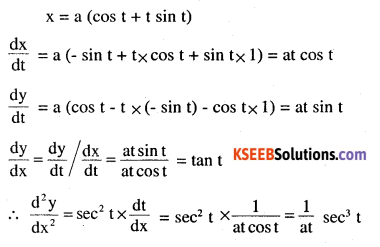
Question 18.
If f (x) = |x|3, show that fn (x) exists for all real x and find it.
Answer:

![]()
Question 19.
Using mathematical induction prove that \(\frac{d}{d x}\left(x^{n}\right)=n x^{n-1}\) for all positive integers n.
Answer:

Question 20.
Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines.
Answer:
sin (A + B) = sin A cos B + cos A sin B
Diff : w:r.to B

cos(A +b) = cos A cos B – sin A sin B
hence cosine formulae
Question 21.
Does there exist a function which is continuous everywhere but not differentiable at exactly two points ? Justify your answer.
Answer:


![]()
Question 22.
It
\(\left|\begin{array}{ccc}{\mathbf{f}(\mathbf{x})} & {\mathbf{g}(\mathbf{x})} & {\mathbf{h}(\mathbf{x})} \\{\mathbf{1}} & {\mathbf{m}} & {\mathbf{n}} \\{\mathbf{a}} & {\mathbf{b}} & {\mathbf{c}}\end{array}\right|, \text { prove that } \quad \frac{\mathbf{d y}}{\mathbf{d x}}=\left|\begin{array}{ccc}{\mathbf{f}^{\prime}(\mathbf{x})} & {\mathbf{g}^{\prime}(\mathbf{x})} & {\mathbf{h}^{\prime}(\mathbf{x})} \\{1} & {\mathbf{m}} & {\mathbf{n}} \\{\mathbf{a}} & {\mathbf{b}} & {\mathbf{c}}\end{array}\right|\)
Answer:

Question 23.
\(y=e^{a \cos ^{-1} x},-1 \leq x \leq 1\)\(\text { show that }\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-a^{2} y=0\)
Answer:

2nd PUC Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise Additional Questions and Answer
Question 1.
\(\text { If } x=a\left(\cos \theta+\log \tan \frac{\theta}{2}\right), y=a \sin \theta, \text { find } \frac{d y}{d x} \text { at } \theta=\frac{\pi}{4}\) (DB 2011)
Answer:

Question 2.
\(f(x)=\left\{\begin{aligned}\frac{\sin (a+1) x+\sin x}{x}, & x<0 \\c &, x=0 \\\frac{\sqrt{x+b x^{2}}-\sqrt{x}}{b x^{3 / 2}}, & x>0\end{aligned}\right.\)
If f(x) is continuous at x = 0 ,find a,b,c. (CBSE 2011, 2008, 2005)
Answer:


![]()
Question 3.
\(\text { If } y=\cos ^{-1}\left\{\frac{3 x+4 \sqrt{1-x^{2}}}{5}\right\} \text { find } \frac{d y}{d x}\) (CBSE 2010)
Answer:

Question 4.
\(\text { If } x^{y}=e^{x \cdot y}, \text { show that } \frac{d y}{d x}=\frac{\log x}{\{\log (x e)\}^{2}}\)(CBSE 2009)
Answer:

Question 5.
Differentiate
\(\sin ^{-1}\left(\frac{t}{\sqrt{1+t^{2}}}\right) \text { w:r:to }\)
\(\cos ^{-1}\left(\frac{1}{\sqrt{1+t^{2}}}\right)\)
Answer:


![]()
Question 6.
\(\text { If } y=\sin ^{-1}\left[\frac{1-\sqrt{x}}{1+\sqrt{x}}\right]+\sec ^{-1}\left[\cfrac{1+\sqrt{x}}{1-\sqrt{x}}\right], \text { find } \frac{d y}{d x}\)
Answer:

Question 7.
Find the derivative of |x|
Answer:

Question 8.
Diff: log10 x w : r : to logx10
Answer:

Question 9.
\(\text { Let } f(x)=\left\{\begin{array}{ll}{\frac{3|x|+4 \tan x}{x},} & {x \neq 0} \\{k} & {x=0}\end{array}\right.\) is continuos at x = o,find K
Answer:

Question 10.
\(\text { If } y=\sqrt{\sin x+\sqrt{\sin x+\sqrt{\sin x+\ldots \ldots \infty}}} \text { prove }\) that \((2 y-1) \frac{d y}{d x}=\cos x\)(Kerala CET)
Answer:

Question 11.

\(\text { prove that, } \frac{d y}{d x}=\cfrac{(1+y) \cos x+y \sin x}{1+2 y+\cos x-\sin x}\) (Kerala CET)
Answer:

![]()
Question 12.
\(y=(\sqrt{x})^{(\sqrt{x})^{(\sqrt{x}}} \text { show that } \frac{d y}{d x}=\frac{y^{2}}{x(2-y \log x)}\) (Kerala CET)
Answer:
