Students can Download Maths Chapter 8 Application of Integrals Ex 8.2 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 8 Application of Integrals Ex 8.2
2nd PUC Maths Application of Integrals NCERT Text Book Questions and Answers Ex 8.2
Question 1.
Find the area of the circle 4x2 + 4y2 = 9 which is interior to the Parobla x2 = 4y.
Answer:
x2 = 4y is up-ward parabola with vertex (0, 0)
Puting x2 = 4y in 4x2 + 4y2 = 9

4 (4y) + 4y2 = 9
⇒ 4y2 + 16 y – 9 = 0

So required area is 2 x (shaded area is 1st quadrant)
= 2x[(area under circle from (x = o to x = \(\sqrt{2}\) – area under parabola (from x = o to x = \(\sqrt{2}\)]

![]()
Question 2.
Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y2 = 1.
Answer:
(1) (x – 1)2 + y2 =1 is a circle with centre (1,0) and radius 1
(2) x2 + y2 = 1 is circle with circle with centre (0,0) and radius (1)
- As shaded area is required one and is a symmetrical convex curve, so, 2 x area of half of shaded region
- It is symmentrical because radius of both are same

2x (area of curve x2 + y2 = 1 from x = \(\frac{1}{2}\)to x = 1
+ area curve (x -1)2 + y2 = 1 from x = 0 to x = \(\frac{1}{2}\))
As if we do along ‘x’ axis or ‘y’ axis, we get area of 1st quadrant, so to get from 1st and 4th quadrant for a curve is this question we need to multiply by 2.

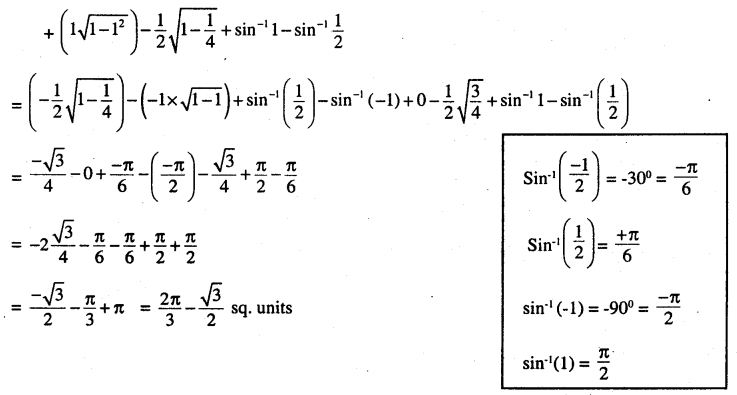

Question 3.
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3.
Answer:
Curve y = x2 + 2 is parabola with vertex (0, 2) (upward parabola)
y = x, line points are (1, 1) (0, 0) (-1, -1) (2, 2) etc
x = 0, line points are (0, 0) (0, 1) (0,-1), (0, 2) (0,-2) etc
x = 3, line points are (3, 0) (3, 1), (3, 2), (3, 3) (3-1) etc…..

so lines meet parabola at :-
line x = 0, y = 2 from y… y = x2 + 2
line x = 3, y = 11
and line x = y, y2 – y + 2 = 0 → y = not pts
so does not meet
Required area is shaded area:-
= (Area under curve y = x2 + 2 from x = 0 to x = 3] – [Area under line x = y from x = 0 to x = 3]

![]()
Question 4.
Using integration find the area of region bounded by the triangle whose vertices are
(-1, 0), (1, 3) and (3, 2).
Answer:
We need line eq: for line AB, BC and AC

so line AB,


Required area is shaded area
⇒[Area under line AB from x = -1 to x = 1
+ Area under BC from x = 1 to x = 3
– Area under AC from x = -1 to x = 3]

Question 5.
Using integration find the area of the triangular region whose sides have the equations y 2x + 1, y = 3x + 1 add x = 4.
Answer:
y = 2x – 1

points are (0, 1), (1, 3) (-1, -1) (4, 9) etc y = 3x + 1
points are (0, 1), (1,4), (-1, -2) (4, 13) etc x = 4
points are (4, 0), (4, 1), (4, 2) etc….

Required area is shaded area:
= [Area under line y = 3x + 1 from (x = 0 to x = 4)]
– [Area under line y = 2x + 1 from (x = 0 to x = 4)]

![]()
Choose the correct answer in the following exercises 6 and 7.
Question 6.
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
(A) 2 (π – 2)
(B) π- 2
(C) 2π – 1
(D)2(π+2)
Answer:
Circle x2 + y2 = 4 his centre (0, 0) and radius 2
line x + y = 2 pts are (1,1) (2, 0) (0, 2) etc………
circle and line intersect at pts.
It can be found by solving the equation
x2 + y2 = 4 put (y = 2 – x)
⇒ x2 + (2 -x)2 = 4 ⇒ 2x2 – 4x + 0 = 0
⇒ 2x2 – 4x = 0 ⇒ x2 – 2x = 0
⇒ (x -2) x = 0 ⇒ x = 0 or x = 2
so y = 2 – x , x = 0 , y = 2 (0, 2)
x = 2 , y = 0 , (2,0)
so they meet at (0, 2) and (2, 0)
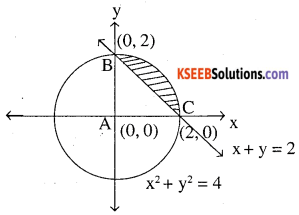
Required area is shaded area:-
(Area under circle x2 + y2 = 4 from x = 0 to x = 2)
– (Area under line x+y = 2 from x = 0 to x = 2)


![]()
Question 7.
Area lying between the curves y2 = 4x and y = 2x is
(A)\(\frac{2}{3}\)
(B)\(\frac{1}{3}\)
(C)\(\frac{1}{4}\)
(D)\(\frac{3}{4}\)
Answer:
Curve y2 = 4x is right parabola with vertex (0, 0)
1. y = 2x is line with pts.
(0,0) (1, 2) (-1,-2) etc…

They meet at pts
y2 = 4x but y = 2x
⇒ (2x)2 = 4x ⇒ 4x2 = 4x ⇒ x = 1, y = 2 (1, 2)
x =0, y = 0 (0, 0)
Required area is shaded area:-
= [Area under curve y2 = 4x from x = 0 to x = 1]
– [Area under line y = 2x from x = 0 to x = 1]
