2nd PUC Statistics Question Bank Chapter 4 Interpolation and Extrapolation

You can Download Chapter 4 Interpolation and Extrapolation Questions and Answers, Notes, 2nd PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Statistics Question Bank Chapter 4 Interpolation and Extrapolation

2nd PUC Statistics Interpolation and Extrapolation One and Two Marks Questions and Answers

Question 1.
Define Interpolation and Extrapolation
Answer:
Interpolation is the technique of estimating the value dependent variable(Y) for any intermediate ) value of the independent variable(X). I
Extrapolation is the technique of estimating the value of dependent variable (Y) any value of independent variable (X) which is outside the given series.

Question 2.
Mention different methods of interpolation.
Answer:

• Binomial expansion method and
• Newton’s advancing difference method

Question 3.
What is interpolation?
Answer:
Interpolation is the technique of estimating the value dependent variable( Y) for any intermediate value of the independent variable(X).

Question 4.
What is meant by extrapolation?
Answer:
Extrapolation is the technique of estimating the value of dependent variable (Y) any value of independent variable (X) which is outside the given series.

Question 5.
Write down the assumptions of interpolation and extrapolation.
Answer:

• The assumptions made in interpolation and extrapolations are:
• There are no sudden jumps in the values of dependent variable(Y) from one period to another(X).
• The rate of change of figures (Y) from one period to another(X) is uniform.
• There will be no consecutive missing values in the series.

Question 6.
Differentiate between interpolation and extrapolation.
Answer:
The procedure of estimating the missing value of y for a given value of x, where x is within the limits x0 and xn we use Interpolation. Here “Interpolation is a procedure of estimating the unknown value of dependent variable for a given value of independent variable which is within the limits or the range of the independent variable”.

But if the value of y is to be estimated for a value of x which is outside the limits x, and x, then procedure Extrapolation is used. Here “Extrapolation is a procedure of estimating the unknown value of dependent variable for a given value of independent variable which is outside the limits or the range of the independent variable”

Question 7.
Write down the conditions for application of Binomial expansion method of interpolation.
Answer:
Following conditions are applied binomial interpolation method:

• The X-variable (independent variable) advances by equal intervals say 15, 20, 25, 30 or say 2, 4, 6, 8, 10 etc.
• The value of X for which the value of Y is to be estimated must be one of the values of X.

Question 8.
Write down the formula of Binomial expansion method of for 5 and 6 known values of y.
Answer:
∆⁵₀ or (y – 1)⁵ = y₅ – 5y₄ + 10y₃ – 10y₂ + 5y₁ – y₀ = 0
∆⁶₀ or (y – 1)⁶ = y₆ – 6y₅ + 15y₄ – 20y₃ + 15y₂ – 6y₁ + y₀ = 0

Write the formula to find the value of ‘x’ in finding the missing value of ‘y’ using Newton’s method of interpolation.

Write down the Newton’s formula for interpolation.

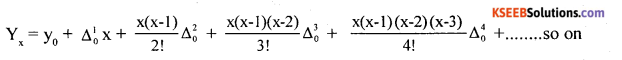
Example 1.
Estimate the production for the year 2010 and 2012 from the following data.

Solution:
Let X and Y be year and production.

Since the known values of ‘Y’ are four, the fourth order leading differences will be zero, i.e. (y- l)⁴ = 0 or Δ⁴ = 0
(y – 1 )⁴ = y₄ – 4y₃ + 6y₂ – 4y₁ + y₀ = 0 (i) and the second equation can be obtained by increasing the suffixes of each term of ‘Y’ by one, keeping the. coefficients same;
we get
y₅ – 4y₄ + 6y₃ – 4y₂ + y₁ = 0 ……(ii)
From equation (i) 52 – 4y₃ + 6 (28) – 4(18) + 8 = 0
52 – 4y₃ + 168 -72 + 8 = 0
So, by simplifying, – 4y₃ = – 156
∴ y₃ = 39 ie. Production for the year 2010 is 139 (tons).
From (ii) y₅ – 4y₄ + 6y₃ – 4y₂ + y₁ = 0; Here y₃ = 39
y₅ – 4 x 52 + 6 x (39) – 4 x 28 + 18 = 0
y₅ – 208 + 234 – 112 + 18 = 0
∴ y₅ = 68 i.e. the production for the year 2012 is 68(tons)

Example 2.
Cost of living indices of a Banglore for some years are given below. Interpolate the missing index number for and

Solution:
Since the known values are 5, the fifth leading differences will be zero, i.e. Δ⁵ = 0
Δ⁵ = (y – 1 )⁵ = y₅ – 5y₄ +10y₃ – 10y₂ + 5y₁ – y₀ = 0 ………….(i)
And the second equation can be obtained by, increasing the suffixes of each term of’y’ by one, keeping the coefficients same;
ie. (y- 1)⁵ = y₆ – 5y₅ + 10y₄ – 10y₃ + 5y₂ – y, = 0 ………. (ii) determine the value of Y₂ from equation (i)
162 – 5(142) +10 (128) – 10y2 + 5(112) – 100 = 0
by simplifying, -10y₂ = -1192
y₂ = 119.2 Hence, the missing Index number for 1990 is 119.2.
From (ii) y₆ – 5(162) + 10(142) – 10(128) + 5(119.2) – 112 = 0 Here y₂ =119.2
y₆ – 810 + 1420 – 1280 + 596- 112 = 0.
∴ y₆ = 186
Hence the cost of living index number for the year 2010 is 186.

Example 3.
Estimate the number of children in the ages 16 and 22 years from the following data:

Solution:
Let X and Y be age and no. of children.

values of y are given, then 5th leading difference will be zero.
Δ⁵₀ = (y – 1 )⁵ = y₅ – 5y₄ + 10y₃ – 10y₂ + 5y₁ – y₀ = 0 …. (i) and the second equation can be obtained as, increasing the suffixes of each term of ‘Y’ by one, keeping the coefficients same; we get :
Δ⁵ = (y – 1)⁵ = y₆ – 5y₅+ 10y₄ – 10y₃ + 5y₂ – y₁ =0 …….(ii)
From equation (i)
y₅ – 5y₄ + 10y₃ – 10y₂ + 5y₁ – y₀ =0
ie„ 98 – 5(88) + 10y3 – 10(65) + 5(55) – 50 = 0
98 – 440 + 10y₃ – 650 + 275 – 50 = 0
So, by simplifying, 10y₃ – 767 = 0
∴ y₃ = 76.7 = 77 children.
From (ii)
i-e, y₆ – 5y₅ + 10y₄ – 10y₃ + 5y₂ – y₁ = 0;
Put y₃= 76.7 we get, y₆ – 5(98) + 10(88) – 10(76.7) + 5(65) – 55 = 0
i.e, y₆ – 490 + 880 – 767 + 325 – 55 = 0
∴ y₆ = 107 children.

Example 4.
Find out the missing values in the following the data.

Solution:

Since 4 known values of y are given, then 4th leading difference may be zero.
Δ⁴₀ = (y – 1 )⁴ = y₄ – 4y₃ + 6y₂ – 4y₁ + y₀ = 0 (i) and the second equation can be obtained
by increasing the suffixes of each term of ‘Y’ by one, keeping the coefficients same; we get:
Δ⁴₁ = (y – l)⁴ = y₅ – 4y₄ + 6y₃ – 4y₂ + y₁ = 0 …………. (ii)
From equation (i) y₄ – 4y₃ + 6y₂ – 4y₁ + y₀ = 0
ie., 38 – 4(33) + 6y2 – 4(20) + 13 = 0
So, by simplifying, 38 – 132 + 6y2 – 80 + 13 = 0 ;
6y₂ – 161
We get y₂ =26.83
From (ii) y₅ – 4y₄ + 6y₃ – 4y₂ + y = 0 = 0
y₅ – 4(38) + 6(33) -4(26.83) + 20 = 0
y₅ – 152 + 198 – 107.32 + 20 = 0
∴ y = 41.32.

Example 5.
Estimate probable life expectation of life of an average Indian at the ages 25 and 40.

Solution:
Since the known values are 5, the estimation is based on the expansion of Δ⁵ = (y – 1)⁵ = 0
∴ Δ⁵= (y – l)⁵ = y₅ – 5y₄ + 10y₃ – 10y₂ + 5y₁ – y₀ = 0
We have to determine the value of y₃;
20.1 – 5(23.1) + 10y₃ – 10(29.1) + 5(32.2) – 35.4 = 0
So, by simplifying, 10y₃ – 260.8 = 0 .
∴ y₃ = 26.08 years.
Hence, the probable expectation of life at the age 25 is 26.08 years.
Now expand (y – l)5 = 0 with change of subscript, keeping coefficients as it is.
y₆ – 5y₅ + 10y₄ – 10y₃ + 5y₂ – y₁ = 0
y₆ – 5(20.1) + 10(23.1) – 10(26.08) + 5(29.1)-32.2 = 0
y₆– 17 = 0, y₆ = 17 years.

Newton’s Method Problems:

Example 1.
The following data given below estimate the number of persons living in the age of 25 years.

Solution:
Since, the value to be estimate does not one of the data(X) So, apply Newton’s method to estimate the number of persons living in the age 15 years.
Since there are 4 known values of y, Prepare the leading difference until Δ³

The first differences in each column are called leading differences.

The number of persons at the age 15 years = 132.375 Example 2.

Example 2.
Below are given the wages earned by workers per day in a certain factory. Calculate the number of emloyees earning up to Rs. 450 per day.

Daily wages	No.of Employees
Up to Rs.300	50
Up to Rs.400	150
Up to Rs.500	300
Up to Rs.600	500
Up to Rs.700	700
Up to Rs.800	800

Solution:
Applying Newton’s method to ascertain number of workers earning upto Rs. 450 per day. Since there are 6 known values of y, so prepare the leading difference table as below:


y_{up to 450} = =50 + 150 + 18.75 + 0 – 1.1718 = 217.58
Thus the number of workers earning up to Rs. 450 is 218.

Example 3.
From the following table find out the number of workers earning salary less than Rs.25(000’s)

Solution:
Convert the data into less than frequency table and find the difference table.
Since there are 6 known values of y, Prepare the leading difference until 5th leading table as below:

Since, the value to be estimate is not in class limits of the data(X) so, apply Newton’s method to estimate the number of workers who are drawing Less than Rs,25(000’s) Salary.

Y(Less than 25) = 125 + 100 – 6.25 – 7 – 3.3594 – 0.2461
The number of workers who are drawing Less than Rs. 25(000’s) = 208.14 = 208.

Example 4.
From the following data interpolate the value for X = 8.

Solution:
Since, the value to be estimate is not one of the value of X series so, apply Newton’s method to estimate the value at X = 8. Since there are 5 known values of y, Prepare the leading difference until 4th leading table as below:

The first differences in each column are called Leading Differences.

Y₈ = 19 +7.5 + 0.875 + 0.0625 – 0.1953;
∴ Y₈ = 27.24.
The value of Y at X = 8 is 27.24.