KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.1

KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.1 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.1.

Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.1

Question 1.
In ∆ABC, right-angled at B, AB = 24 cm., BC = 7 cm. Determine:
i) sin A, cos A
ii) sin C, cos C
Solution:

In ⊥∆ABC, ∠B = 90°
As per Pythagoras theorem
AC² = AB² + BC²
= (24)² + (7) ²
= 576 + 49
AC² = 625
∴ AC = 25 cm

Question 2.
In the given figure, find tan P – cot R.
Solution:

In ⊥∆PQR, ∠Q = 90°
∴ PQ² + QR² = PR²
(12)² + QR² = (13)²
144 + QR² = 169
QR² = 169 – 144
QR² = 25
∴ QR = 5 cm.

Question 3.
If sin A = \(\frac{3}{4}\) calculate cos A and tan A.
Solution:

Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:

Question 5.
Given sec θ = \(\frac{13}{12}\), calculate all other trigonometric ratios
Solution;

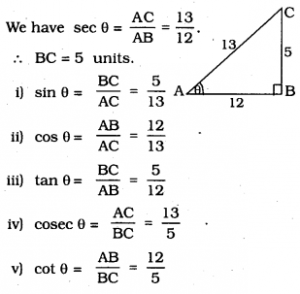
Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:
In ⊥∆ABC, ∠A and ∠B are acute angles. CD ⊥ AB is drawn.

CD is common.
S.S.S. Postulate :
∴ ∆ADC ~ ∆ADB
∴ ∠A = ∠B
∵ “Angles of similar triangles are equiangular.”

Question 7.
If cot θ = \(\frac{7}{8}\), evaluate :
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot²θ
Solution:

Question 8.
If 3 cot A = 4, check whether \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos² A – sin² A or not
Solution:

Question 9.
In ∆ABC, right-angled at B, if tan A =\(\frac{1}{\sqrt{3}}\) find the value of:
i) sin A cos C + cos A sin C
ii) cos A cos C – sin A sin C
Solution:

Question 10.
In ∆PQR, right-angled at Q, PR + QR = 25 cm. and PQ = 5 cm. Determine the values of sin P, cos P and tan P
Solution:
PQ = 5 cm
PR + QR = 25 cm
∴ PR = 25 – QR

PR² = PQ² + QR²
QR² = PR² – PQ²
= (25 – QR)² – (5)²
QR² = 625 – 50QR + QR² – 25
50QR = 600
∴ QR = 12 cm.
∴ PR = 25 – QR = 25 – 12 = 13 cm.
∴ QR = 12 cm
∴ PR = 25 – QR = 25 – 12 = 13 cm

Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
Answer:
False. 60° = \(\sqrt{3}\) > 1

(ii) If sec A = \(\frac{12}{5}\) for some value of angle A.
Answer:
True. because sec A > 1.

(iii) cos A is the abbreviation used for the cosecant of angle A.
Answer:
False. Because cos A is simplified as cos.

(iv) cot A is the product of cot and A.
Answer:
False. cot is ∠A or meaningless. Here,
cot A = \(\frac{\text { Adjacent side }}{\text { Opposite side }}\)

(v) sin θ = \(\frac{4}{3}\) for some angle θ
Answer:
False. because sin θ ≯ 1

We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.1 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.1, drop a comment below and we will get back to you at the earliest.